Τεχνικές τοπολογικές καταστάσεις σε κβαντικές κουκκίδες ημιαγωγών που βασίζονται σε άτομα

 Η υλοποίηση ελεγχόμενων φερμιονικών κβαντικών συστημάτων μέσω κβαντικής προσομοίωσης είναι καθοριστικής σημασίας για την εξερεύνηση πολλών από τα πιο ενδιαφέροντα αποτελέσματα στη φυσική της συμπυκνωμένης ύλης 1 , 2 , 3 . 

Οι κβαντικές κουκκίδες ημιαγωγών είναι ιδιαίτερα ελπιδοφόρες για την κβαντική προσομοίωση, καθώς μπορούν να κατασκευαστούν για να επιτύχουν ισχυρούς κβαντικούς συσχετισμούς.

 Ωστόσο, αν και έχουν αναφερθεί προηγουμένως προσομοίωση του μοντέλου Fermi–Hubbard 4 και του σιδηρομαγνητισμού Nagaoka 5 , το απλούστερο μονοδιάστατο μοντέλο ισχυρά συσχετισμένης τοπολογικής ύλης, το μοντέλο Su–Schrieffer–Heeger (SSH) πολλών σωμάτων 6 , 7 , 8 , 9 , 10 , 11, παρέμεινε μέχρι στιγμής άπιαστο - κυρίως λόγω της πρόκλησης της ακριβούς μηχανικής των αλληλεπιδράσεων μεγάλης εμβέλειας μεταξύ των ηλεκτρονίων για την αναπαραγωγή του επιλεγμένου Hamiltonian. 

Εδώ δείχνουμε ότι για άτομα με ακρίβεια τοποθετημένα σε πυρίτιο με ισχυρό περιορισμό Coulomb, μπορούμε να σχεδιάσουμε τουλάχιστον έξι επιταξιακές πύλες στο επίπεδο για να συντονίσουμε τα επίπεδα ενέργειας σε μια γραμμική διάταξη δέκα κβαντικών κουκκίδων για να συνειδητοποιήσουμε τόσο το ασήμαντο όσο και το Τοπολογικές φάσεις του μοντέλου SSH πολλών σωμάτων. 

Οι ισχυρές επιτόπιες ενέργειες (περίπου 25 χιλιοστοηλεκτρονβολτ) και η ικανότητα κατασκευής πυλών με ακρίβεια υπονανομέτρων σε ένα μοναδικό κλιμακωτό σχέδιο μας επιτρέπουν να συντονίσουμε την αναλογία μεταξύ της μεταφοράς ηλεκτρονίων μεταξύ των κυψελών και των κυψελών για να παρατηρήσουμε σαφείς υπογραφές μιας τοπολογικής φάσης με δύο κορυφές αγωγιμότητας σε πλήρωση τετάρτου, σε σύγκριση με τις δέκα κορυφές αγωγιμότητας της τετριμμένης φάσης.

Κύριος

Υπεραγωγιμότητα, μαγνητισμός 12 , μεταφορά ηλεκτρονίων χαμηλής διάστασης 13 , τοπολογικές φάσεις 14 και άλλες εξωτικές φάσεις της ύλης προκύπτουν λόγω της παρουσίας ισχυρά αλληλεπιδρώντων σωματιδίων μέσα στους κρυστάλλους 15 . Ωστόσο, η πολυπλοκότητα της προσομοίωσης τέτοιων μεγάλων κβαντικών συστημάτων καθίσταται δυσεπίλυτη χρησιμοποιώντας κλασικές μεθόδους υπολογισμού 16 . Μια πολλά υποσχόμενη λύση είναι η κατασκευή ενός φυσικού συστήματος στην ίδια κλίμακα, ώστε να μπορούμε να προσομοιώσουμε αυτά τα αλληλεπιδρώντα φερμιονικά συστήματα 17 , 18 άμεσα, γνωστά ως αναλογική κβαντική προσομοίωση 19 , 20. Το μοντέλο Su–Schrieffer–Heeger (SSH) είναι το πρωτότυπο παράδειγμα τοπολογικής ύλης που περιγράφει ένα μεμονωμένο ηλεκτρόνιο που πηδάει κατά μήκος ενός μονοδιάστατου διμερισμένου πλέγματος με κλιμακωτούς συνδέσμους σήραγγας, v και w , όπως φαίνεται στο Σχ. 1a 21 . Το μοντέλο SSH έχει προσομοιωθεί πειραματικά σε φυσικά συστήματα ποικίλων διαστάσεων από άτομα Rydberg (περίπου 10 μm) έως μηχανικά συστήματα (περίπου 10 mm) (Πίνακας 1). Οι δυνάμεις σύζευξης των διαφόρων προσομοιωτών βρίσκονται στο εύρος νανοηλεκτρονβολτ σε μικροηλεκτρονβολτ, περιορίζοντας την ικανότητά τους να φτάσουν στο πλήρως συνεκτικό καθεστώς. Είναι σημαντικό ότι αυτά τα συστήματα μπορούν εύκολα να επιλυθούν κλασικά καθώς δεν προσομοιώνουν αλληλεπιδράσεις πολλών σωμάτων. Μόλις πρόσφατα παρατηρήθηκε το αλληλεπιδρώντα πολυσωματικό μοντέλο SSH χρησιμοποιώντας άτομα Rydberg με μια αποτελεσματική άπειρη επιτόπια αλληλεπίδραση (σκληροπυρηνικά μποζόνια) 10 . Η ικανότητα ελέγχου της ισχύος αλληλεπίδρασης, ωστόσο, είναι κρίσιμη για τη διερεύνηση των φερμιονικών συστημάτων 22 , 23 .

• Δημοσίευσε:22 Ιουνίου 20

M. Kiczynski ,
ΣΚ Γκόρμαν ,
H. Geng ,
MB Donnelly ,
Y. Chung ,
Υ. Αυτός ,
JG Keizer &
Σίμονς ΜΟΥ 

• Λεπτομέριες Η υλοποίηση ελεγχόμενων φερμιονικών κβαντικών συστημάτων μέσω κβαντικής προσομοίωσης είναι καθοριστικής σημασίας για την εξερεύνηση πολλών από τα πιο ενδιαφέροντα αποτελέσματα στη φυσική της συμπυκνωμένης ύλης 1 , 2 , 3 . Οι κβαντικές κουκκίδες ημιαγωγών είναι ιδιαίτερα ελπιδοφόρες για την κβαντική προσομοίωση, καθώς μπορούν να κατασκευαστούν για να επιτύχουν ισχυρούς κβαντικούς συσχετισμούς. Ωστόσο, αν και έχουν αναφερθεί προηγουμένως προσομοίωση του μοντέλου Fermi–Hubbard 4 και του σιδηρομαγνητισμού Nagaoka 5 , το απλούστερο μονοδιάστατο μοντέλο ισχυρά συσχετισμένης τοπολογικής ύλης, το μοντέλο Su–Schrieffer–Heeger (SSH) πολλών σωμάτων 6 , 7 , 8 , 9 , 10 , 11, παρέμεινε μέχρι στιγμής άπιαστο - κυρίως λόγω της πρόκλησης της ακριβούς μηχανικής των αλληλεπιδράσεων μεγάλης εμβέλειας μεταξύ των ηλεκτρονίων για την αναπαραγωγή του επιλεγμένου Hamiltonian. Εδώ δείχνουμε ότι για άτομα με ακρίβεια τοποθετημένα σε πυρίτιο με ισχυρό περιορισμό Coulomb, μπορούμε να σχεδιάσουμε τουλάχιστον έξι επιταξιακές πύλες στο επίπεδο για να συντονίσουμε τα επίπεδα ενέργειας σε μια γραμμική διάταξη δέκα κβαντικών κουκκίδων για να συνειδητοποιήσουμε τόσο το ασήμαντο όσο και το Τοπολογικές φάσεις του μοντέλου SSH πολλών σωμάτων. Οι ισχυρές επιτόπιες ενέργειες (περίπου 25 χιλιοστοηλεκτρονβολτ) και η ικανότητα κατασκευής πυλών με ακρίβεια υπονανομέτρων σε ένα μοναδικό κλιμακωτό σχέδιο μας επιτρέπουν να συντονίσουμε την αναλογία μεταξύ της μεταφοράς ηλεκτρονίων μεταξύ των κυψελών και των κυψελών για να παρατηρήσουμε σαφείς υπογραφές μιας τοπολογικής φάσης με δύο κορυφές αγωγιμότητας σε πλήρωση τετάρτου, σε σύγκριση με τις δέκα κορυφές αγωγιμότητας της τετριμμένης φάσης.Υπεραγωγιμότητα, μαγνητισμός 12 , μεταφορά ηλεκτρονίων χαμηλής διάστασης 13 , τοπολογικές φάσεις 14 και άλλες εξωτικές φάσεις της ύλης προκύπτουν λόγω της παρουσίας ισχυρά αλληλεπιδρώντων σωματιδίων μέσα στους κρυστάλλους 15 . Ωστόσο, η πολυπλοκότητα της προσομοίωσης τέτοιων μεγάλων κβαντικών συστημάτων καθίσταται δυσεπίλυτη χρησιμοποιώντας κλασικές μεθόδους υπολογισμού 16 . Μια πολλά υποσχόμενη λύση είναι η κατασκευή ενός φυσικού συστήματος στην ίδια κλίμακα, ώστε να μπορούμε να προσομοιώσουμε αυτά τα αλληλεπιδρώντα φερμιονικά συστήματα 17 , 18 άμεσα, γνωστά ως αναλογική κβαντική προσομοίωση 19 , 20. Το μοντέλο Su–Schrieffer–Heeger (SSH) είναι το πρωτότυπο παράδειγμα τοπολογικής ύλης που περιγράφει ένα μεμονωμένο ηλεκτρόνιο που πηδάει κατά μήκος ενός μονοδιάστατου διμερισμένου πλέγματος με κλιμακωτούς συνδέσμους σήραγγας, v και w , όπως φαίνεται στο Σχ. 1a 21 . Το μοντέλο SSH έχει προσομοιωθεί πειραματικά σε φυσικά συστήματα ποικίλων διαστάσεων από άτομα Rydberg (περίπου 10 μm) έως μηχανικά συστήματα (περίπου 10 mm) (Πίνακας 1). Οι δυνάμεις σύζευξης των διαφόρων προσομοιωτών βρίσκονται στο εύρος νανοηλεκτρονβολτ σε μικροηλεκτρονβολτ, περιορίζοντας την ικανότητά τους να φτάσουν στο πλήρως συνεκτικό καθεστώς. Είναι σημαντικό ότι αυτά τα συστήματα μπορούν εύκολα να επιλυθούν κλασικά καθώς δεν προσομοιώνουν αλληλεπιδράσεις πολλών σωμάτων. Μόλις πρόσφατα παρατηρήθηκε το αλληλεπιδρώντα πολυσωματικό μοντέλο SSH χρησιμοποιώντας άτομα Rydberg με μια αποτελεσματική άπειρη επιτόπια αλληλεπίδραση (σκληροπυρηνικά μποζόνια) 10 . Η ικανότητα ελέγχου της ισχύος αλληλεπίδρασης, ωστόσο, είναι κρίσιμη για τη διερεύνηση των φερμιονικών συστημάτων 22 , 23 .

Εικ. 1: Πραγματοποίηση του μοντέλου SSH σε δότες φωσφόρου που έχουν σχεδιαστεί με ακρίβεια σε πυρίτιο.

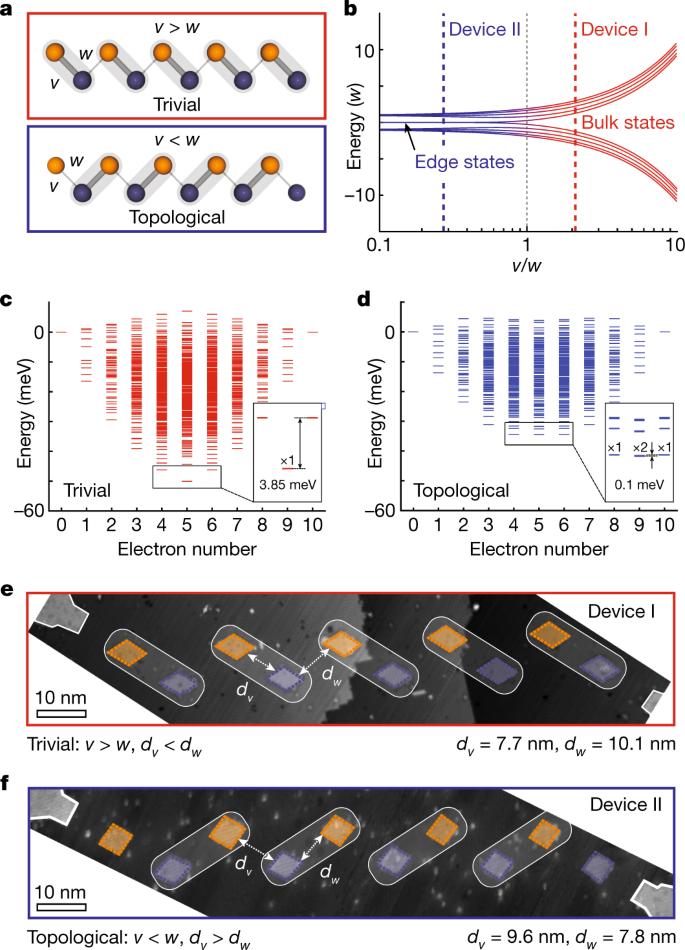
a , Ένα διμερισμένο μονοδιάστατο πλέγμα με κλιμακωτά πλάτη αναπήδησης (σύζευξη σήραγγας) v και w . Ο πίνακας αποτελείται από δύο υποπλέγματα όπου υπάρχει μια τετριμμένη φάση, v  >  w (πάνω) και μια τοπολογική φάση v  <  w (κάτω). b , Ενεργειακό φάσμα ενός σωματιδίου του μοντέλου SSH για μια γραμμική διάταξη δέκα κβαντικών κουκκίδων ως συνάρτηση του λόγου σύζευξης interdot v / w . Για v / w  < 1, υπάρχουν μηδενικής ενέργειας τοπολογικές ακμές καταστάσεις, ενώ η ασήμαντη περίπτωση v / w  > 1 παρουσιάζει ένα κενό διέγερσης.c , d , Υπολογισμένο ενεργειακό φάσμα πολλών ηλεκτρονίων στη τετριμμένη ( c ) και την τοπολογική ( d ) φάση για διαφορετικούς αριθμούς ηλεκτρονίων κατά την πλήρωση τετάρτου. Η τετριμμένη διάταξη παρουσιάζει μια ενιαία θεμελιώδη κατάσταση με πέντε ηλεκτρόνια περίπου 3,85 meV κάτω από τις καταστάσεις τεσσάρων και έξι ηλεκτρονίων, ενώ η τοπολογική φάση παρουσιάζει έναν σχεδόν τετραπλάσιο εκφυλισμό που περιλαμβάνει τέσσερα, πέντε (διπλά εκφυλισμένα) και έξι ηλεκτρόνια. e , f , Μικρογραφία σάρωσης σήραγγας για τις τετριμμένες ( e ; συσκευή I) και τοπολογικές ( f ; συσκευή II) φάσεις. Οι ελαφρύτερες περιοχές δείχνουν την ανοιχτή λιθογραφική μάσκα υδρογόνου. Οι συσκευές αποτελούνται από μια συστοιχία N = 10 κβαντικές κουκκίδες περιορισμένες στο Coulomb με κλιμακωτές αποστάσεις πλησιέστερου γείτονα, συζευγμένες σε σήραγγα σε ένα καλώδιο πηγής (αποχέτευσης) στην αρχή (τέλος) της διάταξης που περιγράφεται με λευκό για την εκτέλεση φασματοσκοπίας πόλωσης. Η συσκευή I έχει σχεδιαστεί για να βρίσκεται στην τετριμμένη φάση με d v  = 7,7 ± 0,1 nm και d w  = 10,1 ± 0,2 nm και η συσκευή II έχει σχεδιαστεί για να βρίσκεται στην τοπολογική φάση με d v  = 9,6 ± 0,4 nm και d w  = 7,8 ± 0,6 nm.

Εικόνα πλήρους μεγέθους

Πίνακας 1 Πειραματικές επιδείξεις του μοντέλου SSH μέχρι σήμερα

Τραπέζι πλήρους μεγέθους

Οι κβαντικές κουκκίδες ημιαγωγών είναι μια αναδυόμενη πλατφόρμα για την κβαντική προσομοίωση ισχυρά συσχετισμένων συστημάτων ηλεκτρονίων 4 , 5 , 20 . Τα αλληλεπιδρώντα ηλεκτρόνια που περιορίζονται σε κβαντικές κουκκίδες έχουν περιγραφεί από το μοντέλο Hubbard 16 που περιλαμβάνει κουλομβικές αλληλεπιδράσεις που περιγράφουν την ενέργεια που απαιτείται για την προσθήκη ηλεκτρονίων στην ίδια (επί τόπου, U ) ή γειτονική (intersite, V ) κβαντική κουκκίδα 24 . Εδώ το intersite hopping διέπεται από τη σύζευξη σήραγγας, t , μεταξύ κβαντικών κουκκίδων, και κάθε κουκκίδα μπορεί να συντονιστεί χρησιμοποιώντας ηλεκτροστατικές πύλες για να αυξήσει ή να μειώσει τα ενεργειακά τους επίπεδα, 

ϵ

$ϵ$ (αναφ. 4). Ειδικά οι δότες φωσφόρου σε πυρίτιο έχουν προταθεί ως πολλά υποσχόμενοι υποψήφιοι για προσομοιωτές, καθώς έχουν μέγεθος νανοκλίμακας με πολύ ισχυρές επιτόπιες ενέργειες ( U  ≈ 25 meV) και μπορούν να κατασκευαστούν ώστε να έχουν ισχυρή ενδιάμεση θέση ( V  ≈ 5 meV) και πηδήματα ( t  ≈ 5 meV) ενέργειες, ενώ λειτουργεί με χαμηλή θερμική ενέργεια k B T  ≈ 0,02 meV (αναφ. 25 ), όπου k B είναι η σταθερά Boltzmann και T η θερμοκρασία, φθάνοντας σε ένα εύρος U / t  ≈ 1− 100 παραμένοντας στο όριο χαμηλής θερμοκρασίας με t / k B T > 10 (αναφ. 23 ). Η ικανότητα επίτευξης του καθεστώτος χαμηλής θερμοκρασίας και ισχυρής αλληλεπίδρασης επιτρέπει την προσομοίωση μιας σειράς πολυπόθητων κβαντικών φάσεων, όπως η υπεραγωγιμότητα 26 και ο αντισιδηρομαγνητισμός 27 , 28 . Παρά την υπόσχεση για προσομοιωτές ημιαγωγών, έχουν παραμείνει σημαντικές προκλήσεις για την προσομοίωση πλήρων κβαντικών συστημάτων. Αυτά σχετίζονται με την ικανότητα ακριβούς σχεδιασμού και συντονισμού τόσο των μεγάλων επιτόπιων ενεργειών αλληλεπίδρασης όσο και των συζεύξεων σήραγγας ώστε να επιτρέπεται ο σχηματισμός μιας καλά καθορισμένης συνεκτικής κατάστασης σε όλο το σύστημα. Συγκεκριμένα, για 10 κβαντικές κουκκίδες, χρειαζόμαστε έλεγχο ακριβείας σε 110 διαφορετικές πειραματικές παραμέτρους που σχετίζονται με U , V , t καιϵ

$ϵ$ .

Σε αυτό το άρθρο, χρησιμοποιούμε την ακρίβεια τοποθέτησης ατομικής ακρίβειας του μικροσκοπίου σάρωσης σήραγγας (STM) για να δημιουργήσουμε κβαντικές κουκκίδες με μεγάλες επιτόπιες ενέργειες ( U  ≈ 25 meV) και ομοιόμορφο μέγεθος για να πραγματοποιήσουμε μια ομοιογενή γραμμική διάταξη για αξιόπιστη ακρίβεια προσομοίωσης. Εάν οι κβαντικές κουκκίδες είναι πολύ μεγάλες, η χωρητική σύζευξη μεταξύ μεμονωμένων κουκκίδων γίνεται πολύ μεγάλη για να τις ελέγξει ανεξάρτητα. Αντίθετα, εάν είναι πολύ μικρά, τότε μια μικρή αλλαγή στον αριθμό των δοτών φωσφόρου εντός της κβαντικής κουκκίδας μπορεί να αλλάξει ουσιαστικά την επιτόπια ενέργεια, οδηγώντας σε τυχαιότητα στη διάταξη. Είναι σημαντικό ότι η δυνατότητα ακρίβειας υπονανομέτρων μας επιτρέπει να αλλάξουμε τις τιμές των v και wμε ανάλυση millielectrovolt ώστε να μπορούμε να εισαγάγουμε αξιόπιστα τόσο τοπολογικά τετριμμένα όσο και τοπολογικά μη τετριμμένα καθεστώτα. Τέλος, μια σημαντική πρόκληση για τις αρχιτεκτονικές κβαντικών κουκκίδων που ορίζονται από πύλη είναι ότι απαιτούν ηλεκτροστατικές πύλες για τη δημιουργία του δυναμικού κβαντικής κουκκίδας και τον έλεγχο των ζεύξεων της σήραγγας που απαιτούν τουλάχιστον περίπου δύο πύλες ανά κβαντική κουκκίδα 29 , 30 , 31 , 32. Με τις κουκκίδες που βασίζονται σε δότη, δεν απαιτούμε αυτές τις πρόσθετες πύλες περιορισμού και απαιτούμε μόνο έξι ηλεκτροστατικές πύλες για τον έλεγχο μιας διάταξης δέκα κβαντικών κουκκίδων, αποφεύγοντας έτσι την περιττή διασταύρωση μεταξύ των πυλών. Για να διασφαλίσουμε τη δημιουργία μιας καλά καθορισμένης κβαντικής κατάστασης σε όλη τη διάταξη, σχεδιάσαμε μια επαναληπτική διαδικασία ευθυγράμμισης μέγιστου ρεύματος για την ευθυγράμμιση των επιπέδων ενέργειας της κβαντικής κουκκίδας εντός περίπου 0,5 meV. Η κβαντική κατάσταση που σχηματίζεται στη συνέχεια μετράται χρησιμοποιώντας φασματοσκοπία πόλωσης μέσω των επίπεδων απαγωγών πηγής και αποστράγγισης. Έχοντας καθορίσει τις απαραίτητες συνθήκες για να σχηματιστεί η επιθυμητή κατάσταση, προσομοιάζουμε τις μονοδιάστατες τοπολογικές φάσεις που σχετίζονται με το αλληλεπιδρώντα μοντέλο SSH 21 .

Το μοντέλο SSH είναι μια από τις απλούστερες γνωστές περιπτώσεις τοπολογικών κβαντικών συστημάτων. Οι ιδιοενέργειες (Εικ. 1β ) του μοντέλου SSH δημιουργούν δύο διακριτές φάσεις που εξαρτώνται από την αναλογία των συζεύξεων της σήραγγας με μια τοπολογική μετάβαση φάσης σε v  =  w . Για το v  >  w , υπάρχει μια τοπολογικά ασήμαντη φάση, όπου το πλέγμα δρα ως μονωτής όγκου με το ηλεκτρόνιο αποτοποθετημένο κατά μήκος της συστοιχίας και ένα ενεργειακό κενό μεταξύ της άνω και της κάτω κατάστασης όγκου. Για v  <  w , υπάρχει μια τοπολογικά μη τετριμμένη φάση - μια τοπολογική φάση που προστατεύεται από συμμετρία - η οποία δημιουργεί δύο καταστάσεις ακμής μηδενικής ενέργειας όπου το ηλεκτρόνιο βρίσκεται στις ακμές θέσεις του πλέγματος33.

Σε προηγουμένως μετρημένες περιπτώσεις του μοντέλου SSH, η συμμετρία σωματιδίου-οπής διατηρήθηκε λόγω έλλειψης αλληλεπιδράσεων μεταξύ ηλεκτρονίων-ηλεκτρονίου 21 . Ωστόσο, οι κβαντικές κουκκίδες στους ημιαγωγούς επηρεάζονται από την ενδιάμεση αλληλεπίδραση Coulomb, V i,j που είναι η αλλαγή στην ενέργεια της κβαντικής κουκκίδας j λόγω της προσθήκης ενός ηλεκτρονίου στην κβαντική κουκκίδα i . Αυτές οι αλληλεπιδράσεις ηλεκτρονίου-ηλεκτρονίου μεγάλης εμβέλειας σπάζουν τη συμμετρία σωματιδίου-οπής, οδηγώντας σε μη εκφυλισμένες καταστάσεις ηλεκτρονίων και οπών 4. Κατά συνέπεια, είναι σημαντικό να ελέγχεται τόσο η πλήρωση ηλεκτρονίων της συστοιχίας όσο και οι αλλαγές στο ηλεκτροστατικό περιβάλλον για να διασφαλιστούν σωστά αποτελέσματα προσομοίωσης. Αυτό απαιτεί όχι μόνο να έχουμε ανεξάρτητο έλεγχο κάθε δυναμικού κβαντικής κουκκίδας αλλά και να αλλάξουμε τα επίπεδα ενέργειας από κοινού - μια τεράστια τεχνολογική πρόκληση για μια τόσο μικρή διάταξη με ισχυρούς συνδέσμους σήραγγας και επιτόπιες ενέργειες ( Συμπληρωματική Ενότητα II ). Ως αποτέλεσμα, θεωρούμε το πλήρες Hamiltonian του εκτεταμένου (χωρίς περιστροφή) μοντέλου Hubbard για μια γραμμική διάταξη Ν κβαντικών κουκκίδων, που δίνεται από

HΣΕ=∑i = 1ΝϵΕγώnΕγώ+∑ΕγώΝΣΕΕγώnΕγώ(nΕγώ−1)+∑ΕγώΝ−1ti , i + 1(ντο†Εγώντοi + 1+ η . γ . ) +∑i , jΝΣΕi , jnΕγώnι,$$H_U=\sum _{i=1}^N{ϵ}_i{n}_i+\sum _i^N{U}_i{n}_i(n_i-1)+\sum _i^{N-1}{t}_{i,i+1}(c_i^{†}{c}_{i+1}+\mathrm{h}.\mathrm{c}.)+\sum _{i,j}^N{V}_{i,j}{n}_i{n}_j,$$

(1)

όπου είναι τα ενεργειακά επίπεδα της i ης κουκκίδας του πίνακα, n i είναι ο τελεστής κατάληψης κουκκίδων, t i , i +1 είναι η σύζευξη της σήραγγας μεταξύ του πλησιέστερου γείτονα i th και i th + 1 κουκκίδες, U i είναι ο επιτόπιος όρος αλληλεπίδρασης Coulomb, V i, j είναι οι ενδιάμεσοι όροι αλληλεπίδρασης Coulomb μεταξύ των κουκκίδων i και j ,  ( c i ) είναι ο τελεστής δημιουργίας (εκμηδενισμού) ενός σωματιδίου στην τοποθεσία i

ϵΕγώ

${ϵ}_i${c}_{i}^{\dagger }ντο†Εγώ

$c_i^{†}$και το hc δηλώνει ερμιτικό συζυγές.

Στο Σχ. 1c, d, δείχνουμε τα 1.024 υπολογισμένα επίπεδα ενέργειας πολλών ηλεκτρονίων με βάση τις δύο πειραματικές συστοιχίες που κατασκευάστηκαν στην τετριμμένη και τοπολογική φάση αντίστοιχα, ταξινομημένα με βάση τον αριθμό των ηλεκτρονίων στη διάταξη κβαντικών κουκίδων κατά την πλήρωση τετάρτου. Για δέκα κβαντικές κουκκίδες, στις οποίες κάθε κουκκίδα μπορεί να φιλοξενήσει δύο ηλεκτρόνια, η πλήρωση τετάρτου αντιστοιχεί στο σημείο όπου υπάρχουν πέντε ηλεκτρόνια που μοιράζονται στις κουκκίδες. Εδώ, εάν η συστοιχία βρίσκεται στην τετριμμένη φάση, τα ηλεκτρόνια απλώς θα τακτοποιηθούν σε κάθε διμερές έτσι ώστε να απλώνονται ομοιόμορφα σε όλη τη διάταξη. Αντίθετα, εάν η διάταξη είναι στην τοπολογική διαμόρφωση κατά την πλήρωση τετάρτου, τέσσερα ηλεκτρόνια διατάσσονται στη μέση της διάταξης (παρόμοια με την τετριμμένη φάση). Ωστόσο, το πέμπτο ηλεκτρόνιο δεν μπορεί να καταλάβει διμερές. Εστιάζουμε στο τέταρτο γέμισμα του πίνακα καθώς οι αλληλεπιδρώντες τοπολογικές καταστάσεις περιλαμβάνουν αυτό το πέμπτο ηλεκτρόνιο που εντοπίζεται σε κάθε άκρο του πίνακα. Στην ασήμαντη φάση (v  >  w ), υπάρχει μια μεμονωμένη εκφυλισμένη θεμελιώδης κατάσταση (πλαίσιο στο Σχ. 1c ) μετατοπισμένη σε ολόκληρη τη συστοιχία με ένα μεγάλο ενεργειακό κενό περίπου 3,85 meV που διαχωρίζει την κατάσταση των πέντε ηλεκτρονίων από τις καταστάσεις τεσσάρων και έξι ηλεκτρονίων. Η τοπολογική φάση ( v  <  w ) παρουσιάζει μια σχεδόν τετραπλάσια εκφυλισμένη (περίπου 0,1 meV) θεμελιώδη κατάσταση (πλαίσιο στο Σχήμα 1d ) που περιλαμβάνει τέσσερα, πέντε (διπλάσια εκφυλισμένα) και έξι ηλεκτρόνια. Η θεμελιώδης κατάσταση αντιστοιχεί σε τέσσερα ηλεκτρόνια στις εσωτερικές οκτώ κβαντικές κουκκίδες της διάταξης με μηδέν, ένα ή δύο επιπλέον ηλεκτρόνια εντοπισμένα στις δύο ακμές κβαντικές κουκκίδες.

Η πειραματική υλοποίηση δύο τέτοιων συστοιχιών φαίνεται στο Σχήμα 1e, f , όπου οι κβαντικές κουκκίδες είναι συζευγμένες με σήραγγα στην πηγή και αποστραγγίζουν τα ηλεκτρόδια για να πραγματοποιηθεί φασματοσκοπία πόλωσης μέσω της διάταξης. Οι περιοχές που περιγράφονται με πορτοκαλί και μπλε χρώμα είναι οι κβαντικές κουκκίδες και οι δύο περιοχές στην αρχή και στο τέλος της διάταξης που περιγράφονται με λευκό είναι οι απαγωγές πηγής και αποστράγγισης. Οι σύνδεσμοι σήραγγας t i , i +1 κατασκευάζονται μέσω του διαχωρισμού μεταξύ σημείων, d i , i +1 και ακολουθούν μια αντίστροφη εκθετική εξάρτηση, (αναφ. 34

ti , i + 1

∝exp(−2

ρε

i , i + 1

/3)

$t_{i,i+1}\propto \exp (-2d_{i,i+1}/3)$). Με την κλιμάκωση της διάταξης κβαντικών κουκκίδων, έχουμε εξασφαλίσει ότι η σήραγγα που δεν είναι ο πλησιέστερος γείτονας καταστέλλεται εκθετικά με εκτιμώμενο t i , i +2 / t i , i +1  ≈ 0,01, διασφαλίζοντας ότι η μεταφορά ηλεκτρονίων πραγματοποιείται σε σειρά μέσω της διάταξης, ενώ μεγιστοποιούνται οι διαφορικοί βραχίονες μοχλού στις κουκκίδες ( Συμπληρωματική Ενότητα I). Το μοντέλο SSH απαιτεί οι σύνδεσμοι της σήραγγας να έχουν εναλλασσόμενες αντοχές για να παρατηρούν τις διαφορετικές τοπολογικές φάσεις ενώ είναι ταυτόχρονα αρκετά μεγάλες ώστε να επιτρέπουν ένα μετρήσιμο ρεύμα μεταφοράς για φασματοσκοπία πόλωσης. Το μέγεθος της κβαντικής κουκκίδας είναι κρίσιμο καθώς το δυναμικό περιορισμού που βιώνει το τελευταίο εξωτερικό ηλεκτρόνιο, και ως εκ τούτου η κυματοσυνάρτηση επικαλύπτεται με τις γειτονικές κβαντικές κουκκίδες, εξαρτάται από τον αριθμό των δοτών που αποτελούν την κβαντική κουκκίδα. Επομένως, κατασκευάζουμε κβαντικές κουκκίδες με εμβαδόν περίπου 25 nm 2 (περίπου 25 δότες φωσφόρου ανά τοποθεσία 35 ). Το μέγεθος νανοκλίμακας των κβαντικών κουκκίδων μας επιτρέπει να επιτύχουμε μεγάλες επιτόπιες ενέργειες περίπου 25 meV, αλλά, το σημαντικότερο, όπου μια μικρή αλλαγή στο μέγεθος της κβαντικής κουκκίδας δεν μεταβάλλει σημαντικά το U ,V , ή t . Ο μικρός διαχωρισμός ≤10 nm μας επιτρέπει επίσης να επιτύχουμε μεγάλες ζεύξεις σήραγγας t  ≈ 1–10 meV για αυτά τα μεγέθη κβαντικών κουκκίδων 35 . Η συσκευή I (Εικ. 1e ) έχει σχεδιαστεί ώστε να βρίσκεται στην τετριμμένη φάση με μέσες κλιμακωτές αποστάσεις κβαντικής κουκκίδας, d v  = 7,7 ± 0,1 nm και d w  = 10,1 ± 0,2 nm, που αντιστοιχεί στο . Η συσκευή II (Εικ. 1f ) έχει σχεδιαστεί για να βρίσκεται στην τοπολογική φάση όπου τώρα κατασκευάζουμε μια μέση κλιμακωτή απόσταση δότη, d v  = 9,6 ± 0,4 nm και d w  = 7,8 ± 0,6 nm, που αντιστοιχεί σε⟨ v / w ⟩ = 2,08

$⟨v/w⟩=2.08$\ langle v / w \ rangle = 0,265 \ langle v / w \ rangle⟨ v / w ⟩ = 0,265

$⟨v/w⟩=0.265$ . Αυτές οι τιμές υπογραμμίζουν την ακρίβεια υπονανοκλίμακας με την οποία μπορούμε να κατασκευάσουμε συσκευές χρησιμοποιώντας λιθογραφία STM, έτσι ώστε να μπορούμε να αλλάξουμε το μεταξύ 0,265 και 2,08 (αναφ. 36 ).⟨ v / w ⟩

$⟨v/w⟩$

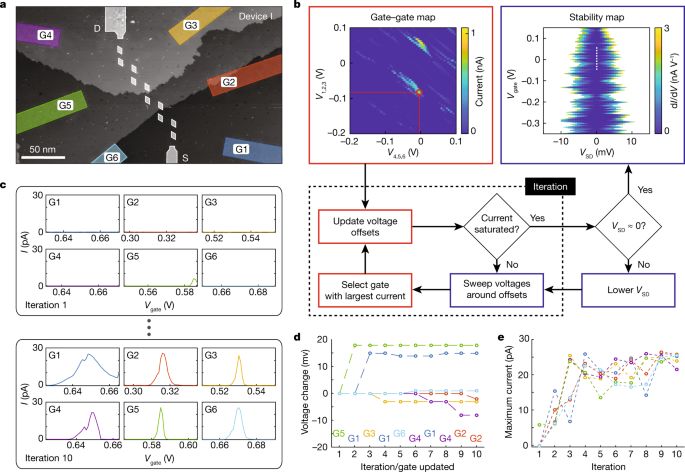
Το σχήμα 2α δείχνει μια εικόνα STM της πλήρους συσκευής I. Εδώ οι περιγραφόμενες ελαφρύτερες περιοχές δείχνουν τη λιθογραφική μάσκα υδρογόνου με έξι χωρητικά συζευγμένες πύλες ελέγχου (G1 έως G6), ζωτικής σημασίας για τον ανεξάρτητο έλεγχο των ενεργειακών επιπέδων των κβαντικών κουκκίδων (δομή πύλης συσκευής II είναι ονομαστικά πανομοιότυπο). Λόγω της μοναδικής γεωμετρίας της συσκευής, οι συνολικοί βραχίονες μοχλού όλων των πυλών που συνδέονται μεταξύ τους σε κάθε κβαντική κουκκίδα έχουν σχεδιαστεί ώστε να συνάδουν με μια απόκλιση μικρότερη από 2,5%. Αυτή η μικρή διακύμανση σημαίνει ότι μπορούμε επίσης να αυξήσουμε το παγκόσμιο επίπεδο ενέργειας ολόκληρης της διάταξης κβαντικών κουκκίδων για φασματοσκοπία πόλωσης για τη μέτρηση των διαφορετικών φάσεων του μοντέλου SSH. Για να ευθυγραμμίσουμε τα επίπεδα ενέργειας των κβαντικών κουκκίδων, χρησιμοποιήσαμε ένα σχήμα ευθυγράμμισης μέγιστου ρεύματος, στο οποίο οι επιμέρους πύλες συντονίζονται όπως περιγράφεται στο Σχήμα.2β . Αυτό επιτυγχάνεται ρυθμίζοντας αρχικά τις τάσεις της πύλης σε μια κορυφή αγωγιμότητας που προσδιορίζεται με σάρωση G1, G2 και G3, έναντι G4, G5 και G6, ενώ μετράται το ρεύμα μέσω της συστοιχίας. Ενώ είναι τοποθετημένη σε αυτή την κορυφή αγωγιμότητας, κάθε πύλη στη συνέχεια σαρώνεται χωριστά γύρω από μια καθορισμένη τιμή, ενώ όλες οι άλλες πύλες διατηρήθηκαν σταθερές, όπως απεικονίζεται στο Σχ. 2γ . Αφού σαρώσετε και τις έξι πύλες σχετικά με την καθορισμένη τάση τους, βρίσκεται η μεγαλύτερη κορυφή ρεύματος και η αντίστοιχη πύλη ενημερώνεται στην τάση στο κέντρο της κορυφής ρεύματος (G5 στην πρώτη επανάληψη που φαίνεται στο Σχ. 2δ ). Στη συνέχεια, όλες οι πύλες σκουπίζονται ξανά, επαναλαμβάνοντας αυτή τη διαδικασία, ενημερώνοντας μία μόνο πύλη τη φορά όπως φαίνεται στο Σχ. 2δ . Εικόνα 2εδείχνει το μέγιστο ρεύμα που μετράται σε κάθε σάρωση πύλης ανά επανάληψη για σταθερή πόλωση πηγής-αποχέτευσης, V SD . Όταν το μέγιστο ρεύμα πέσει, το V SD μειώνεται περαιτέρω και ολόκληρη η διαδικασία επαναλαμβάνεται για να αυξηθεί η ακρίβεια ευθυγράμμισης.

Εικ. 2: Σχέδιο ευθυγράμμισης μέγιστου ρεύματος της διάταξης κβαντικών κουκκίδων χρησιμοποιώντας μόνο έξι πύλες εντός επιπέδου.

a , Μια μικρογραφία STM της συσκευής I, η οποία δείχνει τις έξι πύλες ελέγχου, με την ένδειξη G1 έως G6, που χρησιμοποιούνται για τον συντονισμό των ενεργειακών επιπέδων των κβαντικών κουκκίδων για την παρατήρηση των κορυφών αγωγιμότητας χρησιμοποιώντας φασματοσκοπία πόλωσης. Εδώ μπορούμε να παρατηρήσουμε το ατομικό ύψος βήματος της επιφάνειας του πυριτίου και το μέγεθος νανοκλίμακας της συστοιχίας. σι, Σχηματική απεικόνιση του πρωτοκόλλου που χρησιμοποιείται για την ευθυγράμμιση των κβαντικών κουκκίδων στον πίνακα. Οι κβαντικές κουκκίδες μπορούν να ευθυγραμμιστούν μεταβάλλοντας τις τάσεις που εφαρμόζονται στις πύλες ελέγχου για να συντονιστούν οι κβαντικές κουκκίδες για μέγιστο ρεύμα μέσω της συστοιχίας. Κάθε πύλη ελέγχου ορίζεται αρχικά σε μια συγκεκριμένη τιμή, που επιλέγεται από μια αγώγιμη περιοχή από τον τρέχοντα χάρτη (κόκκινος κύκλος) ενώ αλλάζει τις πύλες G1–G3 και G4–G6 μαζί. Στη συνέχεια, η τάση σε κάθε πύλη σαρώνεται, με τη σειρά της, γύρω από τις αντίστοιχες μέγιστες τιμές ρεύματος, ενώ οι άλλες πύλες διατηρούνται σταθερές. Αφού σαρωθούν όλες οι τάσεις της πύλης, στη συνέχεια ενημερώνεται μια μεμονωμένη τιμή πύλης που αντιστοιχεί στο μέγιστο ρεύμα που μετρήθηκε. Στη συνέχεια, η διαδικασία επαναλαμβάνεται ενημερώνοντας μία πύλη κάθε φορά. Όταν κορεσθεί το μέγιστο ρεύμα, η πόλωση πηγής-αποχέτευσης, V SD, στη συνέχεια μειώνεται και οι πύλες ελέγχου συντονίζονται ξανά για να αυξηθεί το μέγιστο ρεύμα. Μόλις το V SD πλησιάσει το μηδέν, μετράται ένα διάγραμμα σταθερότητας όπως φαίνεται επάνω δεξιά και χρησιμοποιείται η αγωγιμότητα μηδενικής πόλωσης (λευκή γραμμή με διακεκομμένες γραμμές) για σύγκριση με το προσομοιωμένο μοντέλο SSH στο Σχ. 3 . c , Παραδείγματα μεμονωμένων σαρώσεων πύλης στην πρώτη επανάληψη (πάνω) και στη δέκατη επανάληψη (κάτω) για μια σταθερή V SD . d , e , Η τάση σε κάθε πύλη ανά επανάληψη (η πύλη που ενημερώνεται ανά επανάληψη επισημαίνεται στο κάτω μέρος, δ ) και δείχνει το μέγιστο ρεύμα που μετράται σε κάθε σάρωση πύλης ανά επανάληψη ( e ).

Εικόνα πλήρους μεγέθους

Μόλις ευθυγραμμιστούν τα επίπεδα ενέργειας των κβαντικών κουκκίδων, εκτελούμε μια μέτρηση διαγράμματος σταθερότητας μετατοπίζοντας τα ενεργειακά επίπεδα όλων των κβαντικών κουκκίδων για να διερευνήσουμε την κατάληψη ηλεκτρονίων της διάταξης. Το διάγραμμα σταθερότητας μας επιτρέπει να προσδιορίσουμε την κατάληψη ηλεκτρονίων της διάταξης ως συνάρτηση των ενεργειακών επιπέδων των κβαντικών κουκκίδων. Σε μηδενική πόλωση πηγής-αποστράγγισης (διακεκομμένη λευκή γραμμή στο Σχ. 2β ), υπάρχει μόνο αρκετή ενέργεια για να προσθέσετε ένα μόνο ηλεκτρόνιο στον πίνακα κάθε φορά. Σε αυτό το καθεστώς, προσομοιώνουμε το μοντέλο SSH στις δύο συσκευές. Το Σχήμα 3 δείχνει μια σύγκριση των πειραματικών και θεωρητικών αποτελεσμάτων των δύο συσκευών. Το σχήμα 3α δείχνει την υπολογισμένη κανονικοποιημένη αγωγιμότητα μηδενικής πόλωσης ως συνάρτηση του λόγου των συνδέσμων σήραγγας ( v /w ) του πίνακα. Ο σχεδιασμός της συσκευής I στην τετριμμένη φάση δίνεται από τη διακεκομμένη κόκκινη γραμμή , ενώ η συσκευή II στην τοπολογική φάση δίνεται από τη διακεκομμένη μπλε γραμμή .

( ⟨ v / w ⟩ = 2,08 )

$(⟨v/w⟩=2.08)$( ⟨ v / w ⟩ = 0,265 )

$(⟨v/w⟩=0.265)$

Εικ. 3: Πειραματική υπογραφή του μοντέλου SSH σε πίνακες κβαντικών κουκκίδων που έχουν σχεδιαστεί με ακρίβεια.

a , Ένας θεωρητικός χάρτης του κανονικοποιημένου log (αγωγιμότητα) ως συνάρτηση του λόγου των συζεύξεων σήραγγας (με τις ενδιάμεσες αλληλεπιδράσεις Coulomb που δίνονται από μια εξάρτηση 1/ d 1,5 , όπου d είναι ο διαχωρισμός κβαντικής κουκκίδας), με τη συσκευή I που δίνεται από η διακεκομμένη κόκκινη γραμμή και η συσκευή II που δίνονται από τη διακεκομμένη μπλε γραμμή. b , Το ίχνος αγωγιμότητας λήφθηκε σε μηδενική πόλωση πηγής-αποχέτευσης ( V SD  = 0), ενώ μετατοπίζονται τα ενεργειακά επίπεδα όλων των κβαντικών κουκκίδων, στη τετριμμένη φάση. Παρατηρούμε 10 κορυφές αγωγιμότητας που αντιστοιχούν σε μία ζώνη Hubbard με διάκενο περίπου 7,9 meV (περίπου 2 × 3,85 meV) στο τέταρτο πλήρωσης. ντο, Η πιθανότητα κατοχής των ιδιοενεργειών πολλών σωμάτων (και οι 1.024) του μοντέλου Hubbard ως συνάρτηση της συνδυασμένης τάσης πύλης για την τετριμμένη φάση. Οι κορυφές αγωγιμότητας στο b αντιστοιχούν σε μεταβάσεις μεταξύ των διαφορετικών θεμελιωδών καταστάσεων αριθμού ηλεκτρονίων (γκρίζες διακεκομμένες γραμμές), οι οποίες διαχωρίζονται στην τάση πύλης με S k . δ , Χρησιμοποιούμε τις εξαγόμενες τιμές του S k από τα πειραματικά αποτελέσματα για να λάβουμε τις παραμέτρους από το μοντέλο Hubbard (Μέθοδοι) και να τις συγκρίνουμε με τη θεωρία. μι, Στην τοπολογική φάση, παρατηρούμε δύο στενές κορυφές αγωγιμότητας γύρω από την τάση μηδενικής πύλης που προκύπτουν από τις τοπολογικές ακμές κατά το τέταρτο πλήρωσης, ενώ δεν παρατηρούνται κορυφές αγωγιμότητας μακριά από το τέταρτο πλήρωσης (μεταξύ 0 mV και 85 mV στις πύλες). Οι κορυφές αγωγιμότητας (υπάρχουν δύο σε κοντινή απόσταση) που παρατηρούνται γύρω στα 85 mV αντιστοιχούν στην προσθήκη 10 επιπλέον ηλεκτρονίων στη διάταξη και διαχωρίζονται με , που είναι οι μέσες επιτόπιες ενέργειες της συστοιχίας . f , Μια μεγέθυνση των δύο κορυφών αγωγιμότητας της τοπολογικής φάσης που αντιστοιχούν στις μεταβάσεις ηλεκτρονίων m  + 4 →  m  + 5 και m  + 5 →  m  + 6 στη διάταξη που φαίνεται στα 0 mV στο e

⟨ U _⟩

$⟨U⟩$. g , Η πιθανότητα κατάληψης της τοπολογικής φάσης ως συνάρτηση της συνδυασμένης τάσης πύλης. Υπάρχει μια απότομη μετάβαση από τα m  + 4 ηλεκτρόνια όπου δεν υπάρχουν ηλεκτρόνια στις δύο ακμές θέσεις της διάταξης στα m  + 6 ηλεκτρόνια στα οποία οι ακμές θέσεις της συστοιχίας είναι πλήρως κατειλημμένες. Κατά την πλήρωση τετάρτου ( m  + 5 ηλεκτρόνια), υπάρχει μια μη μηδενική πιθανότητα να υπάρχει είτε 4 ( P  ≈ 0,05), 5 ( P  ≈ 0,30 και P  ≈ 0,60 λόγω του διπλού εκφυλισμού) είτε 6 ( P ≈ 0,05) ηλεκτρόνια που υπάρχουν στη συστοιχία ως αποτέλεσμα της σχεδόν τετραπλάσιας εκφυλισμένης βασικής κατάστασης της τοπολογικής φάσης. Αυτό το αξιοσημείωτο χαρακτηριστικό των δύο κορυφών αγωγιμότητας που χωρίζονται από περίπου 0,2 meV είναι η υπογραφή της τοπολογικής φάσης του μοντέλου SSH πολλών σωμάτων.

Εικόνα πλήρους μεγέθους

Το Σχήμα 3β δείχνει την αγωγιμότητα μηδενικής πόλωσης ως συνάρτηση των συνδυασμένων τάσεων σε όλες τις πύλες που λαμβάνονται από την τετριμμένη φάση (συσκευή I) με τον θεωρητικό υπολογισμό να φαίνεται με κόκκινο. Υπάρχουν δέκα κορυφές αγωγιμότητας που αντιστοιχούν σε μια αλλαγή στον συνολικό αριθμό των ηλεκτρονίων στη διάταξη (Εικ. 3c ). Ελέγχουμε την πλήρωση ηλεκτρονίων της διάταξης ρυθμίζοντας τις τάσεις της πύλης για να συντονίσουμε τον αριθμό ηλεκτρονίων από m σε m  + 10 (μισή πλήρωση). Σε ένα τέταρτο πλήρωσης ( m  + 5), υπάρχει ένα κενό στο ενεργειακό φάσμα (7,9 meV, περίπου διπλάσιο από το κενό των 3,85 meV στο Σχήμα 1c ) που αντιστοιχεί στην ενιαία βασική κατάσταση του μοντέλου SSH για την τετριμμένη φάση ( Εικ. 1γ). Από την εκτίμηση του V i,j από την ηλεκτροστατική μοντελοποίηση και την προσαρμογή του μεγέθους της σύζευξης της σήραγγας (Μέθοδοι), μοντελοποιούμε τη διάταξη για να λάβουμε το πλάτος των διαφορετικών περιοχών αριθμού ηλεκτρονίων, S k (πλάτος του m  +  k  →  m  +  k  + 1 περιοχή). Το σχήμα 3δ δείχνει το πλάτος των πειραματικά μετρούμενων περιοχών σταθερότητας, που λαμβάνεται με τον προσδιορισμό της ενέργειας μεταξύ γειτονικών κορυφών αγωγιμότητας, σε σύγκριση με τους θεωρητικούς υπολογισμούς που βασίζονται σε ηλεκτροστατική μοντελοποίηση με λόγο σύζευξης σήραγγας

⟨ v / w ⟩ = 2,08

$⟨v/w⟩=2.08$. Βρίσκουμε εξαιρετική συμφωνία μεταξύ των πειραματικών και των θεωρητικών τιμών. Μικρές αποκλίσεις ( 1 meV) πιθανότατα οφείλονται σε μικρές λανθασμένες ευθυγραμμίσεις των επιπέδων ενέργειας της κβαντικής κουκκίδας, που προκαλεί επιτόπια διαταραχή, προκαλώντας μικρές μετατοπίσεις στις κορυφές αγωγιμότητας, έτσι ώστε η δομή κορυφής να μην είναι πλέον συμμετρικό γύρω από το μηδέν ( Συμπληρωματικό Τμήμα III ).≲

$\lesssim$

Εξετάζουμε τώρα την τοπολογική φάση του μοντέλου SSH (συσκευή II) που φαίνεται στο Σχ. 3e . Η μπλε γραμμή στο Σχ. 3ε αντιπροσωπεύει τη θεωρητική προσαρμογή στο πείραμα, με λόγο σύζευξης σήραγγας . Δείχνουμε μια παρόμοια σάρωση εύρους τάσης όπως για τη συσκευή I, αλλά εδώ παρατηρούμε μόνο δύο σετ κορυφών σε κοντινή απόσταση σε μηδενική τάση πύλης και στα 85,5 mV που αντιστοιχούν στις μέσες επιτόπιες ενέργειες σε όλη τη συστοιχία,

⟨ v / w ⟩ = 0,265

$⟨v/w⟩=0.265$⟨ U _⟩

$⟨U⟩$ = 22,0 ± 3,2 meV. Οι κορυφές αγωγιμότητας από τις καταστάσεις μακριά από το γέμισμα των τετάρτων δεν είναι ορατές καθώς είναι πλέον μετατοπισμένες εντός του μεγαλύτερου μέρους της συστοιχίας με μικρή πιθανότητα να υπάρχουν στις ακραίες κβαντικές κουκκίδες. Ως αποτέλεσμα, η δημιουργία σήραγγας μεταξύ αυτών των καταστάσεων που μοιάζουν με όγκο και των απαγωγών πηγής και αποστράγγισης καταστέλλεται σημαντικά. Στην τοπολογική φάση, το κενό πλήρωσης τετάρτου σχεδόν εξαφανίζεται εντελώς με μια απότομη μετάβαση από τις καταστάσεις m  + 4 σε m  + 6 που δίνεται από μόνο δύο κορυφές αγωγιμότητας που χωρίζονται από περίπου 0,2 meV, που φαίνεται στο Σχ. 3f . Αυτές οι καταστάσεις ηλεκτρονίων αντιστοιχούν εκεί όπου δεν υπάρχουν ηλεκτρόνια ( m  + 4 ηλεκτρόνια) στις κβαντικές κουκκίδες ακμής μέχρι εκεί όπου και οι δύο κουκκίδες είναι κατειλημμένες ( m + 6 ηλεκτρόνια). Είναι σημαντικό κατά την πλήρωση ακριβώς του τετάρτου ( m  + 5 ηλεκτρόνια), υπάρχει μια μη μηδενική πιθανότητα είτε τέσσερα ( P  ≈ 0,05), πέντε ( P  ≈ 0,30 ή P  ≈ 0,60 λόγω του διπλού εκφυλισμού) είτε έξι ( P  ≈ 0,05) ηλεκτρόνια υπάρχουν στη διάταξη ταυτόχρονα λόγω της σχεδόν τετραπλάσιας εκφυλισμένης βασικής κατάστασης, όπως φαίνεται στο Σχ. 3g. Αυτή η αξιοσημείωτη παρατήρηση, ότι σε πόλωση μηδενικής πύλης υπάρχει υπέρθεση του αριθμού ηλεκτρονίων στις ακμές κβαντικές κουκκίδες, είναι αποτέλεσμα της σχεδόν μηδενικής ενέργειας των τοπολογικών καταστάσεων του πίνακα και είναι μια διακριτική ιδιότητα του πολλών σωμάτων Μοντέλο SSH. Καθώς αυτές οι τοπολογικές καταστάσεις εντοπίζονται στις ακραίες κβαντικές κουκκίδες, το ρεύμα που ρέει μέσω της διάταξης αντιστοιχεί σε ένα ηλεκτρόνιο που κινείται από τη μια πλευρά της διάταξης στην άλλη χωρίς να καταλαμβάνει καμία από τις εσωτερικές κβαντικές κουκκίδες. Αυτή η μοναδική ιδιότητα είναι άμεση συνέπεια της τοπολογίας που είναι ενσωματωμένη στο μοντέλο SSH όπως επιβεβαιώνεται από την κορυφή διπλής αγωγιμότητας στο Σχ. 3f .

Συμπερασματικά, έχουμε παρατηρήσει σαφείς υπογραφές των τοπολογικών καταστάσεων του αλληλεπιδρώντος μοντέλου SSH σε κβαντικές κουκκίδες ημιαγωγών. Για να το επιτύχουμε αυτό, κατασκευάσαμε με ακρίβεια δύο συσκευές με ανάλυση υπονανομέτρων που αποτελούνται από μια γραμμική διάταξη δέκα κβαντικών κουκκίδων που βασίζονται σε δότη, με κλιμακωτούς συνδέσμους σήραγγας πλησιέστερου γείτονα. Ο σχεδιασμός ελάχιστης πύλης των επιταξιακών συσκευών μας επιτρέπει τόσο μεμονωμένη όσο και καθολική ευθυγράμμιση όλων των ενεργειακών επιπέδων των κβαντικών κουκκίδων, έτσι ώστε η φασματοσκοπία πόλωσης να μπορεί να ανιχνεύσει τις τοπολογικές φάσεις της συστοιχίας. Είναι σημαντικό ότι επιβεβαιώνουμε την ύπαρξη της μονοδιάστατης τοπολογικής φάσης στο τέταρτο πλήρωσης

( ⟨ v / w ⟩ = 0,265 )

$(⟨v/w⟩=0.265)$με την παρατήρηση δύο αλληλεπικαλυπτόμενων κορυφών στην αγωγιμότητα μηδενικής προκατάληψης που αντιστοιχεί στον σχεδόν τετραπλάσιο εκφυλισμό του μοντέλου SSH πολλών σωμάτων. Για την τετριμμένη φάση , παρατηρούμε δέκα κορυφές αγωγιμότητας μηδενικής πόλωσης που αντιστοιχούν σε μη εντοπισμένες καταστάσεις σε ολόκληρη τη συστοιχία με ένα ενεργειακό κενό γύρω από το τέταρτο πλήρωσης λόγω της μεγάλης σύζευξης interdot περίπου 3,5 meV. Ο σχεδιασμός χαμηλής πυκνότητας πύλης και ο χαμηλός θόρυβος 37 που παρουσιάζονται σε αυτές τις πλήρως επιταξιακές συσκευές προσφέρουν μια πολλά υποσχόμενη πλατφόρμα για την προσομοίωση συστημάτων ηλεκτρονίων ισχυρά αλληλεπιδρώντων για εφαρμογές κβαντικής χημείας 19( ⟨ v / w ⟩ = 2,08 )

$(⟨v/w⟩=2.08)$. Οι μελλοντικές εργασίες θα επικεντρωθούν στην επέκταση του μεγέθους των συστοιχιών κβαντικών κουκκίδων, στην ενσωμάτωση αισθητήρων φορτίου και στην επέκταση των προσομοιώσεων σε κατασκευασμένα δισδιάστατα πλέγματα 38 .

Μέθοδοι

Κατασκευή συσκευής

Οι συσκευές κατασκευάστηκαν σε υπόστρωμα φυσικού πυριτίου τύπου p 1–10 Ω cm. Το υπόστρωμα παρασκευάστηκε μέσω μιας σειράς ανόπτησης υψηλής θερμοκρασίας, έως 1.100 °C, ακολουθούμενη από ελεγχόμενη ψύξη στους 330 °C, με αποτέλεσμα μια (2 × 1) ανακατασκευασμένη επιφάνεια. Το υπόστρωμα στη συνέχεια τερματίστηκε με ατομικό υδρογόνο, το οποίο μπορεί να εκροφηθεί επιλεκτικά χρησιμοποιώντας το άκρο STM, αφήνοντας μια λιθογραφική μάσκα υδρογόνου που αντιπροσωπεύει τη συσκευή. Μετά τη λιθογραφία STM, το υπόστρωμα εκτέθηκε σε ένα πρόδρομο αέριο φωσφίνης (PH 3 ), στο οποίο ο φώσφορος απορροφήθηκε και ενσωματώθηκε, στους 350 °C, στις εκτεθειμένες περιοχές. Στη συνέχεια, η συσκευή ενθυλακώθηκε με 40 nm φυσικού πυριτίου χρησιμοποιώντας επιταξία μοριακής δέσμης με ρυθμό περίπου 0,125 nm min -1. Μια πιο λεπτομερής περιγραφή της λιθογραφίας υδρογόνου STM και της περαιτέρω επεξεργασίας της συσκευής για την ηλεκτρική επαφή της συσκευής μπορείτε να βρείτε στις αναφορές. 42 , 43 , 44 .

Ρύθμιση πειραματικής μέτρησης

Οι ηλεκτρικές μετρήσεις πραγματοποιήθηκαν σε θερμοκρασίες Millkelvin μέσα σε ένα ψυγείο αραίωσης. Οι δύο συσκευές μετρήθηκαν σε διαφορετικά ψυγεία. Η συσκευή Ι μετρήθηκε σε ψυγείο με θερμοκρασία βάσης περίπου 10 mK και η συσκευή II μετρήθηκε σε ψυγείο με θερμοκρασία βάσης περίπου 100 mK. Εκτεταμένα δεδομένα Εικ. 1δείχνει μια σχηματική εικόνα των ηλεκτρικών συνδέσεων στη συσκευή. Για να πραγματοποιηθούν οι μετρήσεις, πηγές τάσης συνδέθηκαν με την πηγή και τις πύλες, για τον έλεγχο των χημικών τους δυνατοτήτων, και το ρεύμα μεταφοράς μετρήθηκε μέσω της αποχέτευσης. Το ρεύμα αποστράγγισης ενισχύθηκε και μετατράπηκε σε σήμα τάσης χρησιμοποιώντας έναν ενισχυτή ρεύματος χαμηλού θορύβου μεταβλητής απολαβής FEMTO DLPCA-200 με ένα φίλτρο χαμηλής διέλευσης 10 Hz. Το σήμα του φίλτρου στη συνέχεια ψηφιοποιήθηκε χρησιμοποιώντας ένα πλαίσιο λήψης δεδομένων National Instrument (NIDAQ). Οι πηγές τάσης που χρησιμοποιήθηκαν για τις δύο συσκευές ήταν διαφορετικές. Για τη συσκευή I, η τάση πηγής δημιουργήθηκε από το βοηθητικό ενός ενισχυτή κλειδώματος Stanford Research Systems SR830 DSP και διαιρέτη αντίστασης 1/50 σε θερμοκρασία δωματίου, ενώ οι τάσεις πύλης δημιουργήθηκαν από δύο NIDAQ. Η συσκευή II μετρήθηκε σε διαφορετικό ψυγείο αραίωσης και είχε διαφορετική πειραματική διάταξη. Η τάση πηγής δημιουργήθηκε από ένα NIDAQ και έναν διαιρέτη αντίστασης τάσης θερμοκρασίας δωματίου 1/50. Οι τάσεις των πυλών 1, 2 και 3 δημιουργήθηκαν επίσης από το NIDAQ, ενώ οι πύλες 4, 5 και 6 τάσεις δημιουργήθηκαν η καθεμία από μια προγραμματιζόμενη πηγή συνεχούς ρεύματος Yokogawa 7651. Οι διαφορετικές πηγές τάσης που χρησιμοποιούνται για τη μέτρηση των διαφορετικών συσκευών δεν θα πρέπει να επηρεάζουν τα αποτελέσματα των μετρήσεων με θεμελιώδη τρόπο.

Υπολογισμός των παραμέτρων του εκτεταμένου μοντέλου Hubbard

Ο πίνακας κβαντικών κουκκίδων μπορεί να περιγραφεί από το εκτεταμένο μοντέλο Hubbard με το Hamiltonian που δίνεται στην εξίσωση ( 1 ). Για να λυθεί θεωρητικά το εκτεταμένο μοντέλο Hubbard και να υπολογιστούν οι παραμέτρους του πίνακα, τα δεδομένα προσαρμόστηκαν χρησιμοποιώντας ένα πακέτο python ανοιχτού κώδικα QmeQ 45 . Η κβαντική κουκκίδα Hamiltonian περιγράφεται από τις καταστάσεις ενός σωματιδίου και τα στοιχεία του πίνακα Coulomb, Το Hamiltonian κατασκευάζεται στη βάση Fock 45 , 46 , για παράδειγμα,

∑

Ν

i = 1ϵΕγώnΕγώ

+

∑Ν−1Εγώti , i + 1

(

ντο†Εγώντοi + 1

+ η . γ . )

${\sum }_{i=1}^N{ϵ}_i{n}_i+{\sum }_i^{N-1}{t}_{i,i+1}(c_i^{†}{c}_{i+1}+\mathrm{h}.\mathrm{c}.)$∑

Ν

i , j

ΣΕ

i , jnΕγώnι

.

${\sum }_{i,j}^N{V}_{i,j}{n}_i{n}_j.$|0010101110⟩

$|0010101110⟩$, όπου το 1 υποδηλώνει ένα ηλεκτρόνιο σε αυτήν την κβαντική κουκκίδα και το 0 υποδηλώνει ότι η κβαντική κουκκίδα δεν είναι κατειλημμένη και διαγωνίζεται ακριβώς για να ληφθούν οι ακριβείς ιδιοκαταστάσεις πολλών σωμάτων , . Το ρεύμα μεταφοράς μέσω του πίνακα κβαντικών κουκκίδων υπολογίζεται στη συνέχεια αριθμητικά χρησιμοποιώντας την κύρια εξίσωση Pauli. Η συστοιχία θεωρείται ότι είναι ασθενώς συζευγμένη με τις απαγωγές πηγής και αποστράγγισης σε θερμοκρασία, T , με πυκνότητα καταστάσεων που ακολουθεί μια κατανομή Fermi, f ( E ).| ένα⟩

$|a⟩$

H=∑

ΚΑΙ

ένα

| a⟩⟨a |

$H=\sum E_a|a⟩⟨a|$

Ανάλογα με το διάγραμμα μη αλληλεπιδρώντος επιπέδου ενέργειας που φαίνεται στο Σχ. 1β , υπολογίσαμε επίσης το διάγραμμα στάθμης ενέργειας του συστήματος αλληλεπίδρασης. Όπως και με το Σχ. 3α , υποθέτουμε ότι οι ενδιάμεσοι όροι Coulomb ακολουθούν μια εξάρτηση d −1,5 47 και ότι τα ενεργειακά επίπεδα των κβαντικών κουκκίδων συντονίζονται μέσω . Εκτεταμένα δεδομένα Το σχήμα 2 δείχνει το ενεργειακό φάσμα για μια συστοιχία δέκα θέσεων για τις καταστάσεις ηλεκτρονίων m  + 4, m  + 5 και m  + 6 κατά την πλήρωση τετάρτου, δείχνοντας το πιο πολύπλοκο φάσμα διεγερμένης κατάστασης των καταστάσεων πολλών σωμάτων του η συστοιχία.

ϵΕγώ

=−

∑

Ν

ι

ΣΕ

i , j

${ϵ}_i=-{\sum }_j^N{V}_{i,j}$

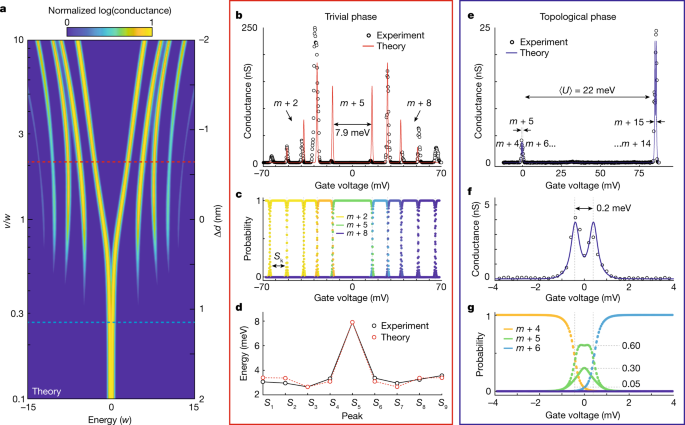
Για v / w  > 1, κατά την πλήρωση τετάρτου ( m  + 5 ηλεκτρόνια), υπάρχει ένα μεγάλο κενό μεταξύ του εδάφους m  + 5 και των χαμηλότερων m  + 4 και m  + 6 ηλεκτρονίων καταστάσεων με μία μόνο θεμελιώδη κατάσταση (με την ένδειξη «χύμα καταστάσεις' ανάλογες με το Σχ. 1β ). Με την αλλαγή των συζεύξεων της σήραγγας έτσι ώστε v / w  < 1, η θεμελιώδης κατάσταση εκφυλίζεται διπλά με m  + 5 ηλεκτρόνια (με την ένδειξη «ακραίες καταστάσεις» ανάλογες με το Σχ. 1β ). Εδώ το κενό πλήρωσης τετάρτου μειώνεται σημαντικά με αποτέλεσμα σχεδόν εκφυλισμένες καταστάσεις με διαφορετικούς αριθμούς ηλεκτρονίων. Το μικρό ενεργειακό χάσμα στο v /w  < 1, παρατηρείται στο ίχνος αγωγιμότητας στο Σχ. 3f και αντανακλά τις ενδιάμεσες αλληλεπιδράσεις Coulomb που υπάρχουν στο σύστημα.

Στο Σχ. 3β και στο Σχ. 3ε , δείχνουμε τον θεωρητικό υπολογισμό της αγωγιμότητας μέσω της διάταξης κβαντικών κουκκίδων που προσαρμόζεται στα πειραματικά δεδομένα για τις τετριμμένες και τοπολογικές φάσεις, αντίστοιχα. Στον θεωρητικό υπολογισμό, θεωρούμε έναν πίνακα δέκα σημείων χωρίς περιστροφή στο καθεστώς όπου μπορεί να υπάρχει το πολύ ένα ηλεκτρόνιο σε καθεμία από τις κβαντικές κουκκίδες. Η μεταφορά ηλεκτρονίων περιορίζεται στη διαδοχική διάνοιξη σήραγγας μέσω της διάταξης, ως αποτέλεσμα της μηχανικής του σχεδιασμού της συσκευής, και μόνο ένα ηλεκτρόνιο μπορεί να διέλθει μέσω των κβαντικών κουκκίδων. Δεν επιτρέπονται συμβάντα συν-σηράγγων υψηλότερης τάξης, καθώς η μεροληψία πηγής-αποχέτευσης είναι αρκετά μικρή, καθιστώντας έγκυρη την επιλογή της κύριας εξίσωσης Pauli. Όλοι οι ενδοτοπικοί όροι αλληλεπίδρασης Coulomb, V i,j, περιλαμβάνονται και υπολογίζονται ρυθμίζοντας τα επίπεδα ενέργειας των κουκκίδων έτσι ώστε .

ϵΕγώ

=−

∑

Ν

ι

ΣΕ

i , j

${ϵ}_i=-{\sum }_j^N{V}_{i,j}$

Οι παράμετροι σύζευξης σήραγγας και αλληλεπίδρασης Coulomb ενδιάμεσης θέσης του εκτεταμένου μοντέλου Hubbard λαμβάνονται με προσαρμογή στις μετρούμενες κορυφές αγωγιμότητας στην ασήμαντη φάση και χρησιμοποιώντας τις μετρούμενες αποστάσεις από το STM και την ηλεκτροστατική μοντελοποίηση. Η τετριμμένη φάση χρησιμοποιήθηκε για την προσαρμογή, καθώς σε αυτή τη φάση μπορούν να παρατηρηθούν και οι δέκα κορυφές αγωγιμότητας, ενώ για την τοπολογική φάση παρατηρούνται μόνο δύο κορυφές αγωγιμότητας. Οι κορυφές αγωγιμότητας στην τετριμμένη φάση στο Σχ. 3β αντιστοιχούν σε μεταβάσεις μεταξύ διαφορετικών θεμελιωδών καταστάσεων αριθμού σωματιδίων, οι οποίες διαχωρίζονται στην τάση πύλης με S k (ο διαχωρισμός τάσης μεταξύ του k και του k  + 1 αριθμού σωματιδίων). Αυτοί οι διαχωρισμοί κορυφής, S k, κυριαρχούνται από τις αντοχές σύζευξης σήραγγας, v και w , και τις ενδιάμεσες αντοχές αλληλεπίδρασης Coulomb, V i,j . Χρησιμοποιώντας τις εξαγόμενες τιμές του S k από τα πειραματικά αποτελέσματα, προσαρμόζουμε το συνολικό μέγεθος της σύζευξης σήραγγας και των ενδιάμεσων αλληλεπιδράσεων Coulomb (διατηρώντας τις θεωρητικά καθορισμένες τάσεις ως συνάρτηση της απόστασης) για να βρούμε τις παραμέτρους που εμφανίζονται στους  Συμπληρωματικούς Πίνακες 4-6 .

Η σύζευξη της σήραγγας, t , κατασκευάζεται μέσω του διαχωρισμού δότη interdot, d , και ακολουθεί μια εκθετική εξάρτηση, t  =  t M exp(−2 d /3) eV, όπου το μέγεθος σύζευξης της σήραγγας t M  = 0,1742 για ένα 1P–2P σύστημα κβαντικών κουκκίδων 34 . Αναμένουμε μια παρόμοια εξάρτηση του t ως συνάρτηση της απόστασης διαχωρισμού μεταξύ σημείων. Ωστόσο, το t M χρησιμοποιείται τώρα ως παράμετρος προσαρμογής καθώς είναι γνωστό ότι εξαρτάται από τον κρυσταλλογραφικό προσανατολισμό των κβαντικών κουκκίδων με v (περίπου ) και w (περίπου

⟨100⟩

$⟨100⟩$⟨120⟩

$⟨120⟩$ ) που έχουν διαφορετικούς παράγοντες κλιμάκωσης λόγω των διαφορετικών αξόνων μεταξύ σημείων. Ο συμπληρωματικός Πίνακας 6 δείχνει τις αποστάσεις και τις συνδέσεις σήραγγας για τις δύο συσκευές, με (1.702, 2.460) για την τετριμμένη φάση και (0,146, 0,539) για την τοπολογική φάση. Η καλύτερη προσαρμογή στις κορυφές αγωγιμότητας μηδενικής πόλωσης επιτυγχάνεται όταν οι σύνδεσμοι της σήραγγας w είναι περίπου διπλάσιοι από τους συνδέσμους v για την ίδια απόσταση ( t M, w  ≈ 2 t M, v⟨ v / w ⟩ = 2,08

$⟨v/w⟩=2.08$⟨ v / w ⟩ = 0,265

$⟨v/w⟩=0.265$). Αυτή η γωνιακή εξάρτηση από τη σύζευξη της σήραγγας μεταξύ μεμονωμένων δωρητών είναι μια πολύ γνωστή συνέπεια του κρυσταλλικού πλέγματος πυριτίου 48 , 49 , 50 . Ωστόσο, τώρα έχει παρατηρηθεί άμεσα για κβαντικές κουκκίδες μεγαλύτερου μεγέθους. Αυτή η πρόσθετη γνώση θα βοηθήσει σε μελλοντικούς πειραματικούς σχεδιασμούς για την τελειότερη μηχανική των συνδέσμων της σήραγγας.

Οι εξαγόμενες παράμετροι σύζευξης σήραγγας δίνουν άριστες προσαρμογές στα πειραματικά δεδομένα όπως φαίνεται στο Σχ. 3b, e , με το Σχήμα 3d να δείχνει μια σύγκριση των διαχωρισμών κορυφής, Sk , για τα πειραματικά και θεωρητικά δεδομένα. Μικρές διακυμάνσεις μεταξύ των πειραματικών και των θεωρητικών δεδομένων μπορούν να αποδοθούν σε σφάλματα στην ηλεκτροστατική μοντελοποίηση και σε μικρές μετατοπίσεις στις ευθυγραμμίσεις των κβαντικών κουκκίδων.

Η παρουσία ενδοτοπικών αλληλεπιδράσεων Coulomb προκαλεί μια διάσπαση περίπου 0,2 meV που παρατηρείται στις τοπολογικές καταστάσεις όπως φαίνεται στο Σχ. 3f . Εκτεταμένα δεδομένα Το Σχήμα 3 δείχνει την υπολογιζόμενη αγωγιμότητα για την τοπολογική φάση για τις μεταβαλλόμενες ενδιάμεσες αντοχές αλληλεπίδρασης Coulomb, V i,j , με τιμές που δίνονται στους  Συμπληρωματικούς Πίνακες 5, 6 . Χωρίς ενδιάμεσες αλληλεπιδράσεις Coulomb, παρατηρείται μια μοναδική κορυφή αγωγιμότητας (Εκτεταμένα δεδομένα Σχήμα 3a ), ενώ η συμπερίληψη των ενδιάμεσων αλληλεπιδράσεων Coulomb οδηγεί σε δύο κορυφές αγωγιμότητας, στις οποίες ο διαχωρισμός μεταξύ των κορυφών αυξάνεται με την αύξηση των V i,j. Εκτός από την παρουσία των ενδιάμεσων αλληλεπιδράσεων Coulomb, μια μικρή διάσπαση (περίπου 0,04 meV) στις τοπολογικές καταστάσεις θα προέκυπτε λόγω του μη μηδενικού λόγου v / w και του πεπερασμένου μήκους της αλυσίδας. Εδώ οι τοπολογικές καταστάσεις, που εντοπίζονται εκθετικά στα αντίθετα άκρα της αλυσίδας, έχουν μια πεπερασμένη επικάλυψη. Αυτός ο μικρός διαχωρισμός, όπως παρουσιάζεται στο Εκτεταμένα Δεδομένα Σχήμα 3α , είναι, ωστόσο, πολύ μικρός για να παρατηρηθεί πειραματικά.

Διαθεσιμότητα δεδομένων

Τα δεδομένα που σχετίζονται με αυτή τη μελέτη είναι διαθέσιμα από τον αντίστοιχο συγγραφέα κατόπιν εύλογου αιτήματος.

βιβλιογραφικές αναφορές

1. Bardeen, J., Cooper, LN & Schrieffer, JR Θεωρία υπεραγωγιμότητας. Phys. Rev. 108 , 1175–1204 (1957).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   MathSciNet
    
   CAS
    
   ΜΑΘΗΜΑΤΙΚΑ
    
   Αρθρο
    
   Μελετητής Google
    

2. Osheroff, DD, Richardson, RC & Lee, DM Αποδεικτικά στοιχεία για μια νέα φάση του στερεού He 3 . Phys. Αναθ. Lett. 28 , 885-888 (1972).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   Αρθρο
    
   Μελετητής Google
    

3. Klitzing, KV, Dorda, G. & Pepper, M. Νέα μέθοδος για τον προσδιορισμό υψηλής ακρίβειας της σταθεράς λεπτής δομής με βάση την κβαντισμένη αντίσταση Hall. Phys. Αναθ. Lett. 45 , 494-497 (1980).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   Αρθρο
    
   Μελετητής Google
    

4. Hensgens, Τ. et αϊ. Κβαντική προσομοίωση ενός μοντέλου Fermi-Hubbard με χρήση διάταξης κβαντικών κουκκίδων ημιαγωγών. Nature 548 , 70–73 (2017).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   PubMed
    
   Αρθρο
    
   Μελετητής Google
    

5. Dehollain, JP et al. Σιδηρομαγνητισμός Nagaoka που παρατηρήθηκε σε μια πλάκα κβαντικής κουκκίδας. Nature 579 , 528–533 (2020).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   PubMed
    
   Αρθρο
    
   Μελετητής Google
    

6. Atala, Μ. et al. Άμεση μέτρηση της φάσης Zak σε τοπολογικές ζώνες Bloch. Nat. Phys. 9 , 795–800 (2013).

   CAS

    
   Αρθρο
    
   Μελετητής Google
    

7. Meier, EJ, An, FA & Gadway, B. Παρατήρηση της τοπολογικής κατάστασης σολιτονίου στο μοντέλο Su–Schrieffer–Heeger. Nat. Commun. 7 , 13986 (2016).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   PubMed
    
   PubMed Central
    
   Αρθρο
    
   Μελετητής Google
    

8. St-Jean, Ρ. et αϊ. Lasing σε τοπολογικές ακμές καταστάσεις ενός μονοδιάστατου πλέγματος. Nat. Φωτόνιο. 11 , 651–656 (2017).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   Αρθρο
    
   Μελετητής Google
    

9. Chaunsali, R., Kim, E., Thakkar, A., Kevrekidis, P. & Yang, J. Επίδειξη μιας in situ τοπολογικής μετάβασης ζώνης σε κυλινδρικές κοκκώδεις αλυσίδες. Phys. Αναθ. Lett. 119 , 024301 (2017).

   ΔΙΑΦΗΜΙΣΕΙΣ

    
   CAS
    
   PubMed
    
   Αρθρο
    
   Μελετητής Google
    

10. de Léséleuc, S. et al. Παρατήρηση τοπολογικής φάσης προστατευμένης από συμμετρία μποζονίων που αλληλεπιδρούν με άτομα Rydberg. Science 365 , 775–780 (2019).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    MathSciNet
     
    PubMed
     
    ΜΑΘΗΜΑΤΙΚΑ
     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

11. Cai, W. et αϊ. Παρατήρηση τοπολογικών καταστάσεων μονωτή magnon σε υπεραγώγιμο κύκλωμα. Phys. Αναθ. Lett. 123 , 080501 (2019).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

12. Nielsen, E. & Bhatt, RN Νανοκλίμακας σιδηρομαγνητισμός σε μη μαγνητικούς ντοπαρισμένους ημιαγωγούς. Phys. Rev. B 76 , 161202 (2007).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

13. Le, NH, Fisher, AJ & Ginossar, E. Extended Hubbard μοντέλο για μεσοσκοπική μεταφορά σε συστοιχίες δότη σε πυρίτιο. Phys. Αναθ. Β 96 , 245406 (2017).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

14. Le, NH, Fisher, AJ, Curson, NJ & Ginossar, E. Τοπολογικές φάσεις ενός διμερισμένου μοντέλου Fermi–Hubbard για νανοδικτυώματα ημιαγωγών. npj Quantum Inf. 6 , 24 (2020).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

15. Imada, M., Fujimori, A. & Tokura, Y. Μεταβάσεις μετάλλου–μονωτή. Rev. Mod. Phys. 70 , 1039-1263 (1998).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    Αρθρο
     
    Μελετητής Google
     

16. Qin, M., Schäfer, T., Andergassen, S., Corboz, P. & Gull, E. Το μοντέλο Hubbard: μια υπολογιστική προοπτική. Annu. Αναθ. Condens. Ύλη Φυσ. 13 , 275–302 (2022).

17. Feynman, R. Προσομοίωση φυσικής με υπολογιστές. Int. J. Theor. Phys. 21 , 46-488 (1982).

    MathSciNet

     
    Αρθρο
     
    Μελετητής Google
     

18. Cirac, JI & Zoller, P. Στόχοι και ευκαιρίες στην κβαντική προσομοίωση. Nat. Phys. 8 , 264–266 (2012).

    CAS

     
    Αρθρο
     
    Μελετητής Google
     

19. Argüello-Luengo, J., González-Tudela, A., Shi, T., Zoller, P. & Cirac, JI Analogue quantum chemistry simulation. Nature 574 , 215–218 (2019).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    PubMed
     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

20. Altman, Ε. et αϊ. Κβαντικοί προσομοιωτές: αρχιτεκτονικές και ευκαιρίες. PRX Quantum 2 , 017003 (2021).

    Αρθρο

     
    Μελετητής Google
     

21. Su, WP, Schrieffer, JR & Heeger, AJ Solitons σε πολυακετυλένιο. Phys. Αναθ. Lett. 42 , 1698-1701 (1979).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    Αρθρο
     
    Μελετητής Google
     

22. Tasaki, H. The Hubbard model—μια εισαγωγή και επιλεγμένα αυστηρά αποτελέσματα. J. Phys Condens. Matter 10 , 4353-4378 (1998).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    Αρθρο
     
    Μελετητής Google
     

23. Salfi, J. et αϊ. Κβαντική προσομοίωση του μοντέλου Hubbard με προσμίξιμα άτομα σε πυρίτιο. Nat. Commun. 7 , 11342 (2016).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    PubMed Central
     
    Αρθρο
     
    Μελετητής Google
     

24. Wang, X., Yang, S. & Das Sarma, S. Quantum theory of the charge-stability diagram of semiconductor double-quantum-dot systems. Phys. Αναθ. Β 84 , 115301 (2011).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

25. Dusko, A., Delgado, A., Saraiva, A. & Koiller, B. Adequacy of Si:P chains as Fermi–Hubbard simulators. npj Quantum Inf. 4 , 1 (2018).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

26. Maier, T., Jarrell, M., Pruschke, T. & Keller, J. d - wave superconductivity στο μοντέλο Hubbard. Phys. Αναθ. Lett. 85 , 1524–1527 (2000).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

27. Hirsch, JE & Tang, S. Αντισιδηρομαγνητισμός στο δισδιάστατο μοντέλο Hubbard. Phys. Αναθ. Lett. 62 , 591-594 (1989).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

28. Arovas, DP, Berg, E., Kivelson, S. & Raghu, S. The Hubbard model. Annu. Αναθ. Condens. Ύλη Φυσ. 13 , 239–274 (2022).

29. Nichol, JM et αϊ. Πύλη εμπλοκής υψηλής πιστότητας για qubits διπλής κβαντικής κουκκίδας. npj Quantum Inf. 3 , 3 (2017).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

30. Mills, AR et αϊ. Μεταφορά μιας μόνο φόρτισης σε μια μονοδιάστατη σειρά από κβαντικές κουκκίδες πυριτίου. Nat. Commun. 10 , 1063 (2019).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    PubMed Central
     
    Αρθρο
     
    Μελετητής Google
     

31. Yang, CH et αϊ. Λειτουργία κυψέλης μονάδας κβαντικού επεξεργαστή πυριτίου πάνω από ένα Kelvin. Nature 580 , 350–354 (2020).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

32. MacQuarrie, ER et al. Πρόοδος προς ένα χωρητικώς διαμεσολαβούμενο CNOT μεταξύ δύο qubit φόρτισης σε Si/SiGe. npj Quantum Inf. 6 , 81 (2020).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

33. Asbóth, JK, Oroszlány, L. & Pályi, A. The Su – Schrieffer – Heeger (SSH) Model (Springer, 2016).

34. Wang, Y., Chen, C.-Y., Klimeck, G., Simmons, MY & Rahman, R. Πλήρως ηλεκτρικός έλεγχος qubits σπιν ηλεκτρονίων δεσμευμένων σε δότη σε πυρίτιο. Προεκτύπωση στη διεύθυνση https://arxiv.org/abs/1703.05370 (2017).

35. Watson, TF et al. Μεταφορά σε ασύμμετρα συζευγμένες τριπλές κβαντικές κουκκίδες πυριτίου με βάση δότη. Nano Lett. 14 , 1830–1835 (2014).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

36. He, Υ. et αϊ. Μια πύλη δύο qubit μεταξύ ηλεκτρονίων δότη φωσφόρου σε πυρίτιο. Nature 571 , 371–375 (2019).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

37. Kranz, L. et αϊ. Αξιοποίηση ενός μονοκρύσταλλου περιβάλλοντος για την ελαχιστοποίηση του θορύβου φόρτισης στα qubits σε πυρίτιο. Adv. Μητήρ. 32 , 2003361 (2020).

    CAS

     
    Αρθρο
     
    Μελετητής Google
     

38. Wang, Χ. et αϊ. Κβαντική προσομοίωση ενός εκτεταμένου μοντέλου Fermi-Hubbard χρησιμοποιώντας ένα 2D πλέγμα κβαντικών κουκκίδων που βασίζονται σε πρόσμιξη. Προεκτύπωση στη διεύθυνση https://arxiv.org/abs/2110.08982 (2021).

39. Kim, Ε. et αϊ. Κβαντική ηλεκτροδυναμική σε τοπολογικό κυματοδηγό. Phys. Rev. 11 , 011015 (2021).

    CAS

     
    Αρθρο
     
    Μελετητής Google
     

40. Lin, S., Zhang, L., Tian, ​​T., Duan, C.-K. & Du, J. Δυναμική παρατήρηση τοπολογικών καταστάσεων σολιτονίου σε προγραμματιζόμενο νανομηχανικό πλέγμα. Nano Lett. 21 , 1025–1031 (2021).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    Αρθρο
     
    Μελετητής Google
     

41. Kruk, S. et αϊ. Καταστάσεις ακμών και τοπολογικές μεταβάσεις φάσης σε αλυσίδες διηλεκτρικών νανοσωματιδίων. Small 13 , 1603190 (2017).

    Αρθρο

     
    CAS
     
    Μελετητής Google
     

42. Rueß, FJ et al. Υλοποίηση ατομικά ελεγχόμενων συσκευών προσμίξεων σε πυρίτιο. Small 3 , 563–567 (2007).

    PubMed

     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

43. Broome, MA et al. Συσχετισμοί σπιν δύο ηλεκτρονίων σε δότη ακριβείας που τοποθετούνται σε πυρίτιο. Nat. Commun. 9 , 980 (2018).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    PubMed Central
     
    Αρθρο
     
    Μελετητής Google
     

44. Fricke, L. et al. Συνεκτικός έλεγχος qubit σπιν ηλεκτρονίου δότη-μορίου σε πυρίτιο. Nat. Commun. 12 , 3323 (2021).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    PubMed
     
    PubMed Central
     
    Αρθρο
     
    Μελετητής Google
     

45. Kiršanskas, G., Pedersen, JN, Karlström, O., Leijnse, M. & Wacker, A. QmeQ 1.0: ένα πακέτο python ανοιχτού κώδικα για υπολογισμούς μεταφοράς μέσω συσκευών κβαντικής κουκκίδας. Υπολογιστής. Phys. Commun. 221 , 317–342 (2017).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    MathSciNet
     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

46. Lin, HQ, Gubernatis, JE, Gould, H. & Tobochnik, J. Μέθοδοι ακριβούς διαγωνοποίησης για κβαντικά συστήματα. Υπολογιστής. Phys. 7 , 400 (1993).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    Μελετητής Google
     

47. Hogg, M. Scalable Readout and Control of Phosphorus Donor Spin Qubits in Silicon . Διδακτορική διατριβή, UNSW Sydney Australia (2021).

48. Koiller, B., Hu, X. & Das Sarma, S. Ανταλλαγή σε αρχιτεκτονική κβαντικών υπολογιστών με βάση το πυρίτιο. Phys. Αναθ. Lett. 88 , 027903 (2002).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    PubMed
     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

49. Wellard, CJ et al. Σύζευξη ανταλλαγής ηλεκτρονίων για qubit spin μονού δότη στερεάς κατάστασης. Phys. Rev. Β 68 , 195209 (2003).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    Αρθρο
     
    CAS
     
    Μελετητής Google
     

50. Joecker, Β. et αϊ. Προσομοιώσεις αλληλεπίδρασης πλήρους διαμόρφωσης δοτών συζευγμένων με ανταλλαγή σε πυρίτιο χρησιμοποιώντας θεωρία αποτελεσματικής μάζας πολλαπλών κοιλάδων. New J. Phys. 23 , 073007 (2021).

    ΔΙΑΦΗΜΙΣΕΙΣ

     
    CAS
     
    Αρθρο
     
    Μελετητής Google
     

Λήψη παραπομπών

Ευχαριστίες

Η έρευνα υποστηρίχθηκε από τη Silicon Quantum Computing Pty Ltd και το Κέντρο Αριστείας του Αυστραλιανού Ερευνητικού Συμβουλίου για τον Κβαντικό Υπολογισμό και την Τεχνολογία Επικοινωνιών (αριθμός έργου CE170100012). Η MYS αναγνωρίζει μια υποτροφία βραβευμένη με το Αυστραλιανό Ερευνητικό Συμβούλιο.

Πληροφορίες συγγραφέα

Σημειώσεις του συγγραφέα

1. Υ. Αυτός

   Παρούσα διεύθυνση: Shenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology, Shenzhen, Κίνα

Συγγραφείς και Συνεργασίες

1. Κέντρο Αριστείας για τον Κβαντικό Υπολογισμό και την Τεχνολογία Επικοινωνιών, Σχολή Φυσικής, UNSW Σίδνεϊ, Κένσινγκτον, Νέα Νότια Ουαλία, Αυστραλία

   M. Kiczynski, SK Gorman, H. Geng, MB Donnelly, Y. Chung, Y. He, JG Keizer & MY Simmons

2. Silicon Quantum Computing Pty Ltd, UNSW Σίδνεϊ, Kensington, Νέα Νότια Ουαλία, Αυστραλία

   M. Kiczynski, SK Gorman, H. Geng, MB Donnelly, Y. Chung, JG Keizer & MY Simmons

Συνεισφορές

Οι SKG, YH και MYS συνέλαβαν το έργο. Οι MK, HG, MBD, JGK και YC κατασκεύασαν τις συσκευές. Οι MK και SKG πραγματοποίησαν τις μετρήσεις, ανέλυσαν τα δεδομένα και έκαναν τους θεωρητικούς υπολογισμούς. Το χειρόγραφο γράφτηκε από τους MK, SKG, JGK και MYS με τη συμβολή όλων των συγγραφέων. Η MYS επέβλεψε το έργο.

Αντίστοιχος συγγραφέας

Αλληλογραφία με MY Simmons .

Δηλώσεις δεοντολογίας

Ανταγωνιστικά συμφέροντα

Οι συγγραφείς δεν δηλώνουν ανταγωνιστικά συμφέροντα.

Αξιολόγηση από ομοτίμους

Πληροφορίες αξιολόγησης από ομοτίμους

Η Nature ευχαριστεί τον Ingmar Swart και τους άλλους, ανώνυμους, κριτές για τη συμβολή τους στην αξιολόγηση από ομοτίμους αυτού του έργου. Οι αναφορές ομότιμων κριτών είναι διαθέσιμες.

Επιπλέον πληροφορίες

Σημείωση εκδότη Το Springer Nature παραμένει ουδέτερο όσον αφορά τις διεκδικήσεις δικαιοδοσίας σε δημοσιευμένους χάρτες και θεσμικές σχέσεις.

Εκτεταμένα στοιχεία και πίνακες

Εκτεταμένα δεδομένα Εικ. 1 Ρύθμιση πειραματικής μέτρησης.

a , Σχηματική της πειραματικής ρύθμισης για τη Συσκευή I, που δείχνει όλες τις ηλεκτρικές συνδέσεις στη συσκευή. Εμφανίζεται μια εικόνα STM της συσκευής I. Οι τάσεις της πύλης ελέγχονται από ένα NIDAQ και τρία Yokogawa και η τάση της πηγής από το NIDAQ. Το ρεύμα αποστράγγισης (πράσινη γραμμή) ενισχύεται μέσω ενός ενισχυτή χαμηλού θορύβου FEMTO και αποκτάται από το NIDAQ. β , Σχηματική της πειραματικής ρύθμισης για τη Συσκευή II, που δείχνει όλες τις ηλεκτρικές συνδέσεις στη συσκευή. Εμφανίζεται μια εικόνα STM της διάταξης 10 κουκκίδων, η οποία έχει ληφθεί πριν από τη διαμόρφωση των πυλών ελέγχου. Οι τάσεις της πύλης ελέγχονται από δύο NIDAQ και η τάση της πηγής ελέγχεται από έναν ενισχυτή κλειδώματος SR830 DSP. Το ρεύμα αποστράγγισης (πράσινη γραμμή) ενισχύεται μέσω ενός ενισχυτή χαμηλού θορύβου FEMTO και αποκτάται από το NIDAQ.

Εκτεταμένα δεδομένα Εικ. 2 Ενέργειες των καταστάσεων πολλών σωμάτων στο μοντέλο SSH που αλληλεπιδρά γύρω από την πλήρωση τετάρτου.

Οι ενέργειες των m  + 4, m  + 5 και m  + 6 ηλεκτρονίων καταστάσεων για μια διάταξη 10 θέσεων ως συνάρτηση του λόγου σύζευξης της σήραγγας, v / w . Οι ενέργειες υπολογίζονται στο τέταρτο (δηλαδή, η θεμελιώδης κατάσταση είναι πάντα m  + 5 ηλεκτρόνια). Η θεμελιώδης κατάσταση εξελίσσεται από μια μεμονωμένη εκφυλισμένη κατάσταση για v / w > 1 (καταστάσεις που μοιάζουν με όγκο) σε μια διπλή εκφυλισμένη κατάσταση m  + 5 ηλεκτρονίων για v / w < 1 (κατάσταση που μοιάζει με ακμή). Το ενεργειακό κενό πλήρωσης τετάρτου μεταξύ των  θεμελιωδών καταστάσεων ηλεκτρονίων m  + 4 και m + 6 μειώνεται όσο v/ w < 1 με αποτέλεσμα σχεδόν εκφυλισμένες καταστάσεις, που αντικατοπτρίζει το σχεδόν μηδενικό κόστος ενέργειας που σχετίζεται με την προσθήκη ενός ηλεκτρονίου στην τοπολογική φάση της διάταξης, με ένα μικρό ενεργειακό χάσμα λόγω των αλληλεπιδράσεων Coulomb μεταξύ των τοποθεσιών.

Εκτεταμένα δεδομένα Εικ. 3 Διαίρεση της τοπολογικής φάσης λόγω της παρουσίας αλληλεπιδράσεων Coulomb μεταξύ των τοποθεσιών.

Μια σύγκριση των θεωρητικά υπολογισμένων ιχνών αγωγιμότητας (μπλε γραμμές) με τα πειραματικά δεδομένα που παρατηρήθηκαν (κύκλοι) καθώς η ισχύς αλληλεπίδρασης Coulomb στην περιοχή ποικίλλει από, a , χωρίς αλληλεπιδράσεις Coulomb, σε b , 0,5 ×  V i,j , c , V i,j , και d , 2 ×  V i,j. Στην περίπτωση που δεν υπάρχουν αλληλεπιδράσεις Coulomb, παρατηρείται μόνο μία κορυφή στο θεωρητικό ίχνος αγωγιμότητας, η οποία δεν ταιριάζει με τη διάσπαση περίπου 0,2 meV που παρατηρείται στα πειραματικά δεδομένα. Καθώς η ισχύς αλληλεπίδρασης Coulomb αυξάνεται, δύο κορυφές εξελίσσονται με τη διαίρεση μεταξύ των κορυφών να αυξάνεται, με τη διάσπαση περίπου 0,2 meV να ταιριάζει με τα πειραματικά δεδομένα στο c .

Συμπληρωματικές πληροφορίες

Συμπληρωματικές πληροφορίες

Αυτό το αρχείο συμπληρωματικών πληροφοριών περιλαμβάνει συμπληρωματικούς πίνακες 1–6, Εικ. 1–5 και Παραπομπές.

Αρχείο αξιολόγησης από ομοτίμους

Δικαιώματα και άδειες

Ανοικτή πρόσβαση Αυτό το άρθρο αδειοδοτείται με άδεια Creative Commons Attribution 4.0 International License, η οποία επιτρέπει τη χρήση, την κοινή χρήση, την προσαρμογή, τη διανομή και την αναπαραγωγή σε οποιοδήποτε μέσο ή μορφή, αρκεί να αποδίδετε την κατάλληλη πίστωση στον αρχικό δημιουργό και την πηγή, δώστε έναν σύνδεσμο προς την άδεια Creative Commons και υποδείξτε εάν έγιναν αλλαγές. Οι εικόνες ή άλλο υλικό τρίτων σε αυτό το άρθρο περιλαμβάνονται στην άδεια Creative Commons του άρθρου, εκτός εάν αναφέρεται διαφορετικά σε πιστωτικό όριο για το υλικό. Εάν το υλικό δεν περιλαμβάνεται στην άδεια Creative Commons του άρθρου και η χρήση για την οποία προορίζεται δεν επιτρέπεται από νομοθετική ρύθμιση ή υπερβαίνει την επιτρεπόμενη χρήση, θα χρειαστεί να λάβετε άδεια απευθείας από τον κάτοχο των πνευματικών δικαιωμάτων. Για να δείτε ένα αντίγραφο αυτής της άδειας, επισκεφθείτεhttp://creativecommons.org/licenses/by/4.0/.

Επανεκτυπώσεις και Άδειες

Σχετικά με αυτό το άρθρο

Αναφέρετε αυτό το άρθρο

Kiczynski, Μ., Gorman, SK, Geng, Η. et αϊ. Τεχνικές τοπολογικές καταστάσεις σε κβαντικές κουκκίδες ημιαγωγών που βασίζονται σε άτομα. Nature 606, 694–699 (2022). https://doi.org/10.1038/s41586-022-04706-0

Λήψη αναφοράς

• Ελήφθη
  05 Νοεμβρίου 2021

• Δεκτός
  01 Μαρτίου 2022

• Δημοσίευσε
  22 Ιουνίου 2022

• Ημερομηνία έκδοσης
  23 Ιουνίου 2022

• DOI
  https://doi.org/10.1038/s41586-022-04706-0

Μοιραστείτε αυτό το άρθρο

Όποιος μοιράζεστε τον ακόλουθο σύνδεσμο θα μπορεί να διαβάσει αυτό το περιεχόμενο:

Παρέχεται από την πρωτοβουλία κοινής χρήσης περιεχομένου Springer Nature SharedI

https://www.nature.com/articles/s41586-022-04706-0